Как управлять инвестиционным портфелем

Незадолго до создания модели CAPM вместе с другими экономистами Уильям Шарп предложил вариант построения границы эффективных портфелей на основе теории Гарри Марковица. Рекомендованный в 1963 г. метод впоследствии модифицировали — сегодня он известен как индексная модель Шарпа.

Причины появления модели

Главная предпосылка для создания этого метода заключалась в сокращении объема вычислений при среднедисперсионной оптимизации портфеля, которую предложил Гарри Марковиц. Для использования этой модели в качестве входных данных по каждому активу нужно задать следующие параметры:

• ожидаемые доходность и волатильность
• попарную корреляцию доходности актива с другими бумагами в портфеле, которая обычно задается через ковариационную матрицу.

Когда эра компьютеров только зарождалась, последний параметр представлял наибольшую трудоемкость вычисления при большом количестве ценных бумаг в портфеле.

Допустим, n — это количество активов в портфеле, подаваемых на вход. Количество комбинаций двух элементов из выборки n по мере ее увеличения растет достаточно быстро. При 10 бумагах корреляций будет 45, при 100 бумагах — 4950, при 500 бумагах, как в индексе S&P 500, — уже 124 750.

Особенность модели

Шарп предложил считать корреляцию активов не напрямую друг с другом, а через некий бенчмарк — индекс. Логика заключается в том, что большинство акций на фондовом рынке достаточно сильно коррелируют друг с другом из-за наличия общих макрофакторов. При достаточно диверсифицированном портфеле индивидуальная волатильность бумаг взаимно погашается, остается только общая, обусловленная системным риском.

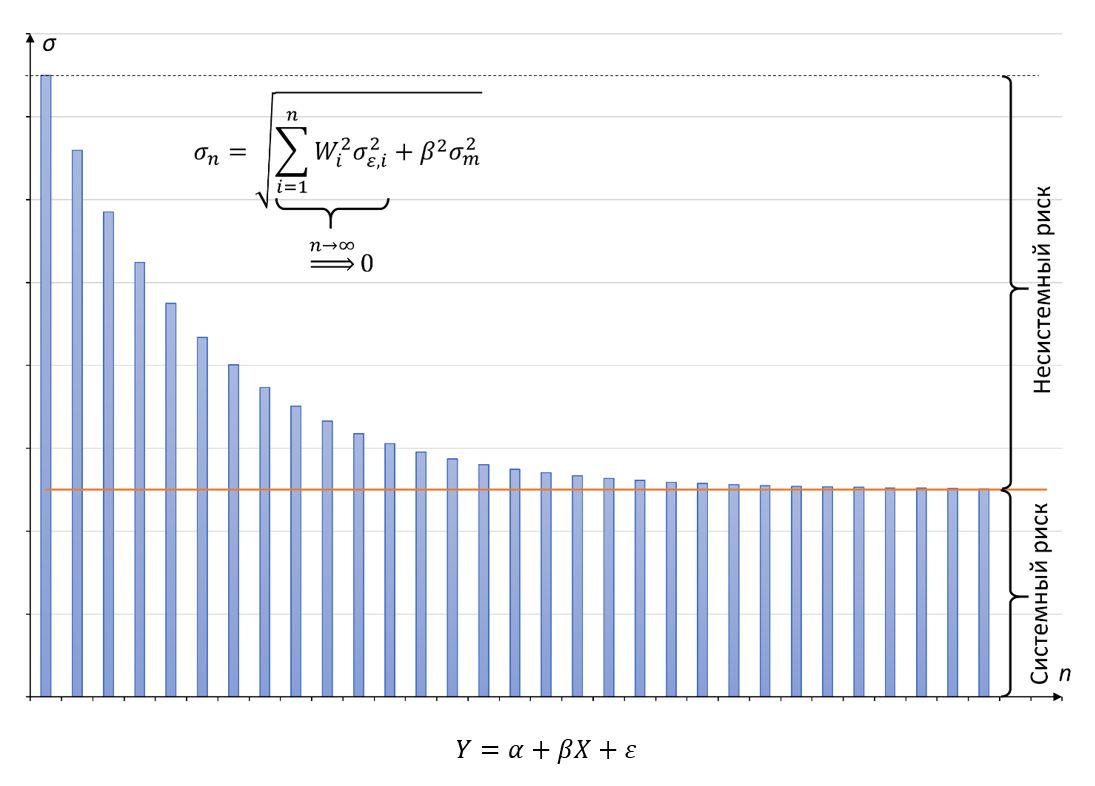
Таким образом, модель Шарпа позволила в разы сократить расчет необходимых входных данных. Сама модель строится на принципах линейного регрессионного анализа, где доходность актива представляется в виде линии регрессии с одним независимым фактором - доходностью рыночного индекса.

Разберем показатели модели подробнее:

• Y — доходность конкретной акции в портфеле за выбранный период
• α — параметр линейной регрессии, называемый коэффициентом «альфа» (не путать с «альфой» в CAPM), показывающий, какая часть доходности акции портфеля не связана с изменениями доходности рыночного портфеля
• β — параметр линейной регрессии, называемый коэффициентом «бета», характеризующий чувствительность доходности акции к изменениям рыночной доходности индекса
• X — доходность рыночного портфеля за тот же период
• ε — случайная ошибка, свидетельствующая о том, что реальные наблюдаемые значения отклоняются от теоретических величин, получаемых с использованием линейной зависимости.

Подставив данные зависимости в формулу Марковица, можно получить новые формулы для доходности и волатильности всего портфеля, выраженные уже через характеристики рынка или индекса.

Формула полной волатильности портфеля (σn) в модели Шарпа показывает, как с увеличением количества бумаг волатильность, обусловленная их внутренней динамикой (σε,i), стремится к нулю. Остается только часть, представляющая системный риск: произведение портфельной «беты» (β) на волатильность рыночного индекса (σm). Wi представляет долю i-й бумаги в портфеле.

Итоги

Граница эффективности Шарпа представляет собой очень точное приближение, или, другими словами, упрощение границы Марковица. Индексная модель Шарпа использует ряд допущений, которые и создают расхождение в оптимальной структуре портфеля в сравнении с моделью Марковица. Прежде всего, это отсутствие корреляции между ошибками текущего и следующего периода, а также между случайными ошибками и рыночной доходностью индекса. Если все эти корреляции равны нулю, то структура портфеля по Марковицу и Шарпу должны совпадать.